Las puertas lógicas son circuitos electrónicos diseñados para obtener resultados booleanos (tipo 0 y 1). Estos resultados se obtienen de operaciones lógicas binarias: la suma y la multiplicación. Son por tanto, la base del circuito digital.
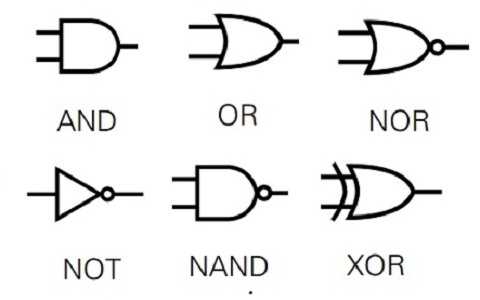
Tenemos puertas AND, OR, NOT, NAND, NOR, XOR, XNOR. Además se pueden conectar entre sí para obtener nuevas funciones.
La ejemplificación de las puertas AND y OR, que son la base del resto es muy comprensible utilizando diagramas de circuitos eléctricos, tal como vimos en el artículo dedicado a los circuitos serie y paralelo.
Si no entendemos mucho de qué estamos hablando, no nos preocupemos mucho. Al llegar al final del artículo la luz habrá iluminado tu mente y comprenderás todas estas explicaciones que ahora mismo te parecen tan extrañas.
Vacía tu mente, que comenzamos.
AND
Llamado también producto lógico.
En el circuito AND los interruptores los conectamos en serie. Veamos su gráfico y comprendamos cuándo se enciende la bombilla.
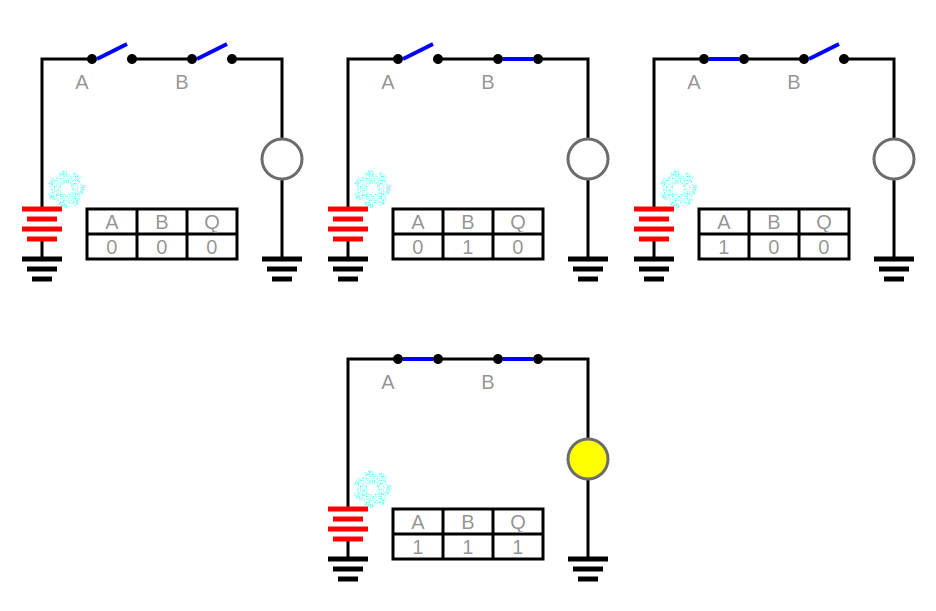
Como podemos observar, tenemos 2 interruptores, el A y el B. ¿Qué diferentes posibilidades tenemos de posicionar esos interruptores? Sólo hay 4, pensadlo bien. Veámoslas:
- Tanto el interruptor A como el B podrían estar abiertos
- El interruptor A podría estar abierto y el B cerrado
- El interruptor A podría estar cerrado y el B abierto
- Tanto el interruptor A como el B podrían estar cerrados
Si el interruptor está abierto, no conducirá la corriente, y por convención, podemos decidir que eso tiene el valor 0. En cambio si el interruptor está cerrado, sí que conduce la corriente, y entonces le daremos el valor 1.
Con estas prerrogativas haremos una tabla que muestre como funciona el circuito al que hemos llamado AND. Esta tabla mostrará las 4 diferentes posiciones de los 2 interruptores.
A esta tabla la llamaremos TABLA DE LA VERDAD.
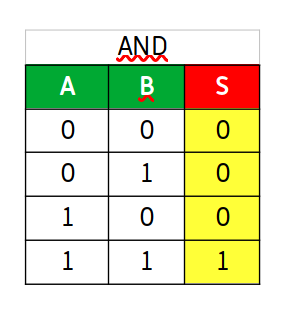
Los enunciados de las columnas son A, B y S. A y B son los interruptores y S es la salida del circuito, es decir, si se enciende la bombilla o no se enciende. A y B pueden estar abiertos o cerrados, es decir en estado 0 (abierto y no conduce la corriente) o en estado 1 (cerrado y conduce la corriente). Y la bombilla puede estar encendida (1) o apagada (0), es decir que S será 0 o 1 dependiendo de si se enciende o no, lo que dependerá de como estén los interruptores.
Este circuito hemos dicho que se le conoce como PRODUCTO LÓGICO y a la vista está que la columna S es el resultado de multiplicar A por B. De ahí, lo del producto lógico. La salida es 1, o lo que es lo mismo, la bombilla se enciende sólo cuando A y B están cerrados. Fijémonos que hemos dicho A y B. Esa y es la que da nombre al circuito: circuito AND.
Si los dos están abiertos no pasa la corriente y no se enciende la bombilla. Si sólo uno de los dos está cerrado tampoco pasa la corriente y tampoco se enciende la bombilla. Únicamente se encenderá si ambos están cerrados, A y B (A and B).
Por tanto, la salida 0 significa que no se enciende la bombilla ya que el circuito no llega a cerrarse y la salida 1 que sí se enciende ya que los electrones hacen el viaje completo.
Su puerta lógica se representa así 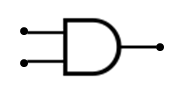
OR
Llamado también suma lógica.
En el circuito OR los interruptores los conectamos en paralelo. Veamos su gráfico y comprendamos cuándo se enciende la bombilla.
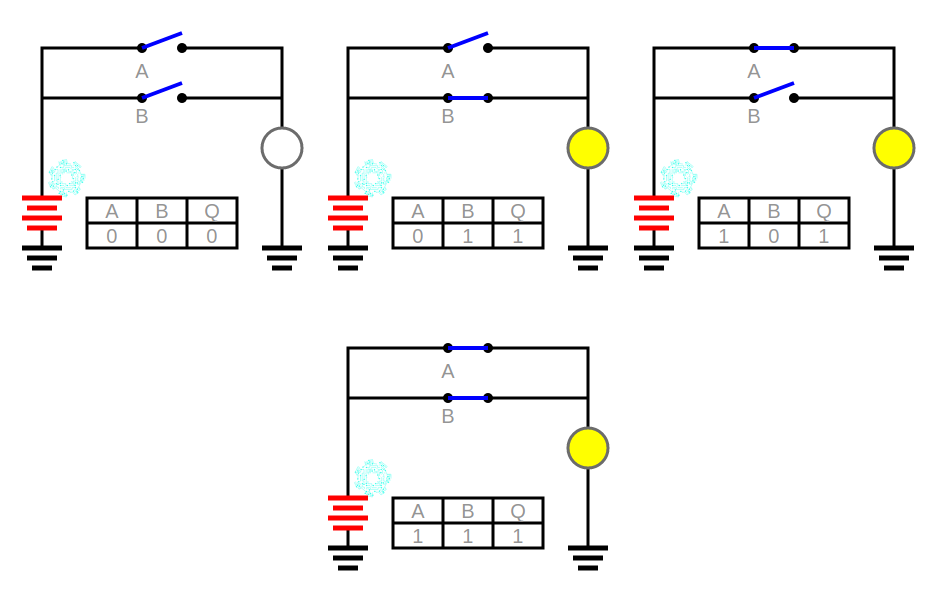
Observemos que tenemos los mismos 2 interruptores. Por tanto, tenemos las mismas 4 posibilidades de posicionarlos que en el circuito AND, pero en este caso la salida será diferente.
Hagamos su TABLA DE LA VERDAD:
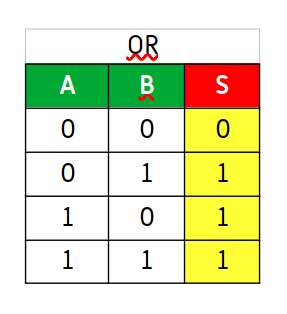
Está claro mirando el circuito con que sólamente es necesario un interruptor cerrado para que la bombilla se ilumine, es decir, el interruptor A, o el B, o ambos. El siguiente gráfico muestra el funcionamiento.
¿Se entiende ahora por qué se le llama circuito OR?
Se le llama también SUMA LÓGICA, porque la salida es la suma de las posiciones de A y B.
Su puerta lógica se representa así 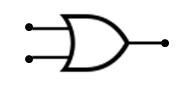
NOT, NAND, NOR, XOR y XNOR
Aglutinamos en este apartado la explicación del resto de puertas lógicas y acabaremos el artículo con un esquema con todas las puertas, sus tablas de la verdad , sus ecuaciones y su simbología.
NOT
El circuito NOT es el circuito conocido como NEGADO o COMPLEMENTO LÓGICO. El negado consiste dar como respuesta el valor contrario al proporcionado. Es decir, devuelve 1 si recibe 0, y 0 si recibe 1.
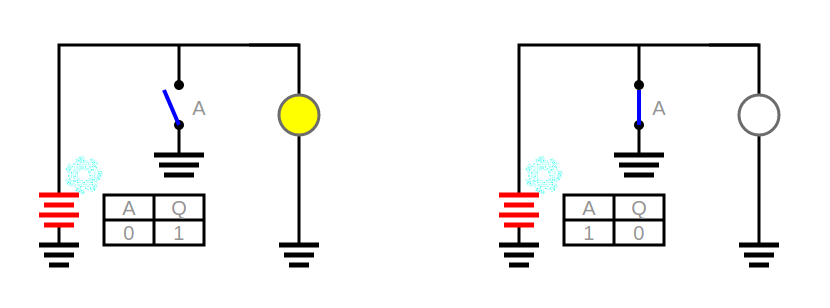
Simple y básico, pero es el fundamento para poder crear nuevos circuitos y tener así un amplio abanico de posibilidades a la hora de combinarlos.
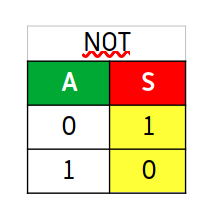
Su puerta lógica se representa así 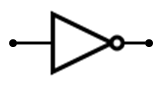
NAND
El circuito NAND es la suma de los circuitos AND y NOT. Es decir, cogemos la salida del circuito AND y hacemos el negado o complemento lógico. Los ceros los cambiamos por unos y los unos por ceros. El circuito sería:
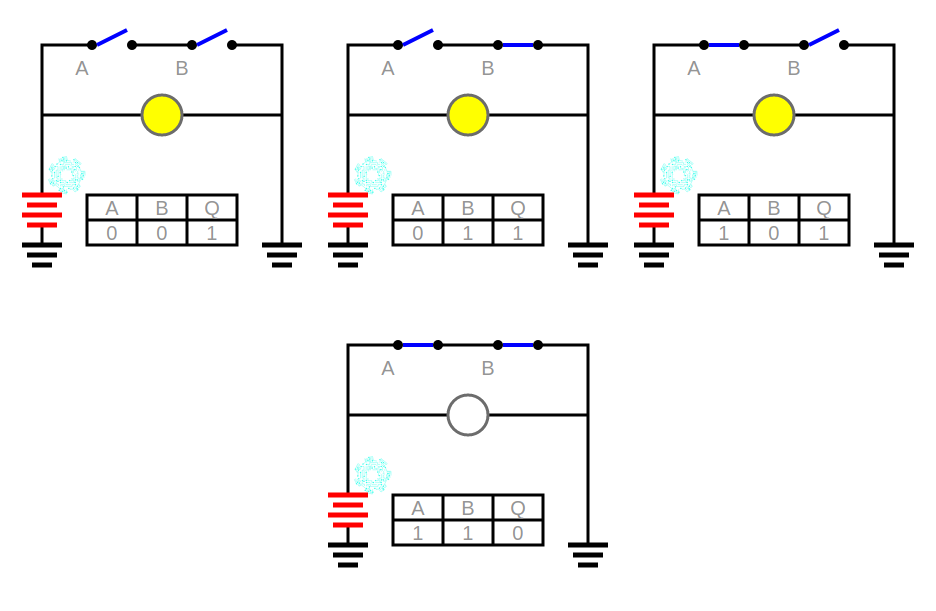
Y su tabla de la verdad,
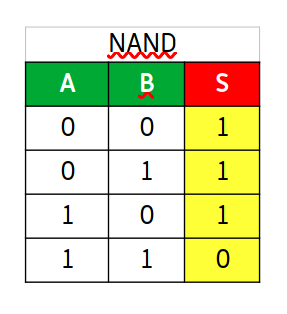
Su puerta lógica se representa así 
NOR
El circuito NOR es la suma de los circuitos OR y NOT. Es decir, cogemos la salida del circuito OR y hacemos el negado o complemento lógico. Los ceros los cambiamos por unos y los unos por ceros.
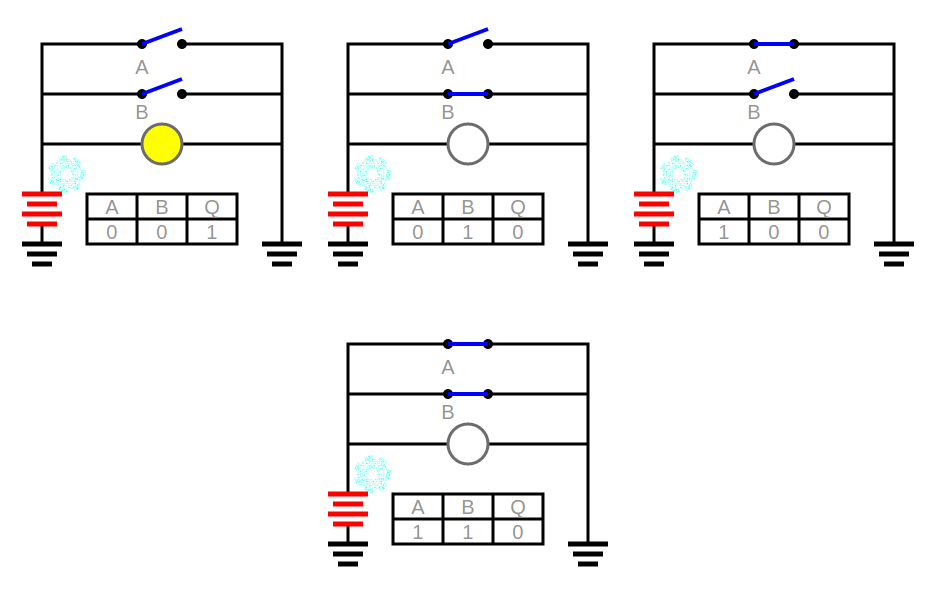
Y su tabla de la verdad es
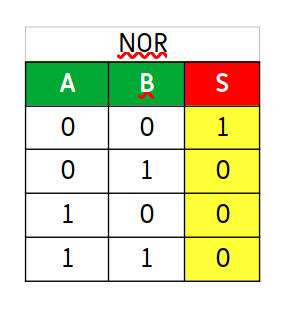
Su puerta lógica se representa así 
XOR
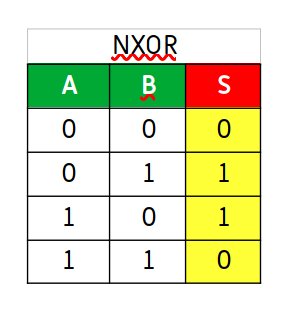
En el circuito XOR da como salida 1 cuando las dos entradas son distintas y 0 cuando son iguales. Es decir, cuando A y B den las combinaciones A=1 B=1 y A=0 B=0, la salida será 0. Si dan las combinaciones A=0 B=1 y A=1 B=0, la salida será 1.
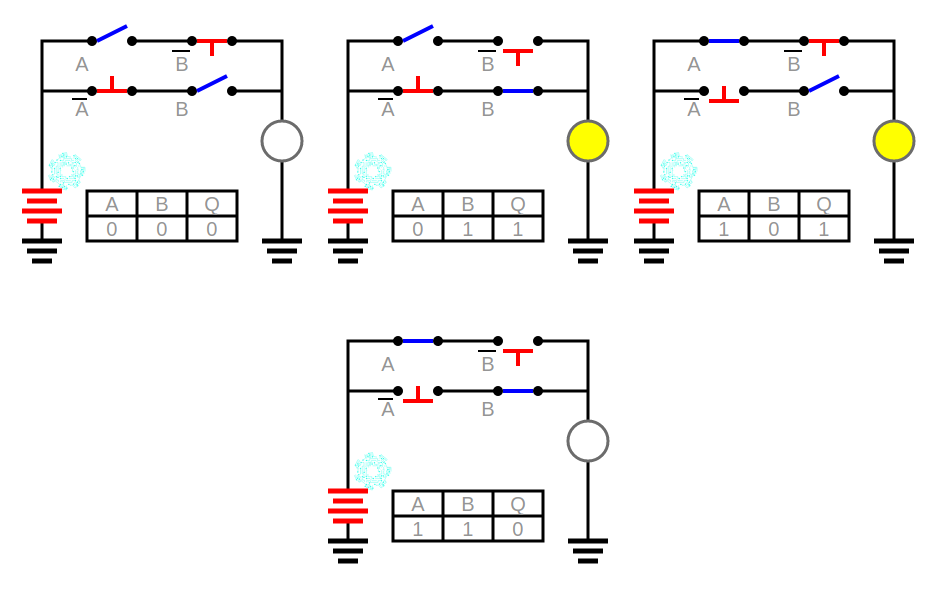
Conocida como OR exclusivo.
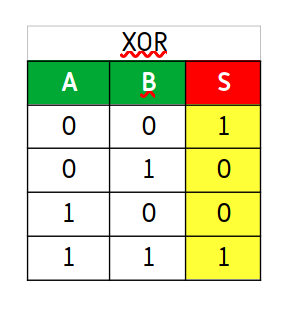
Su puerta lógica se representa así 
XNOR
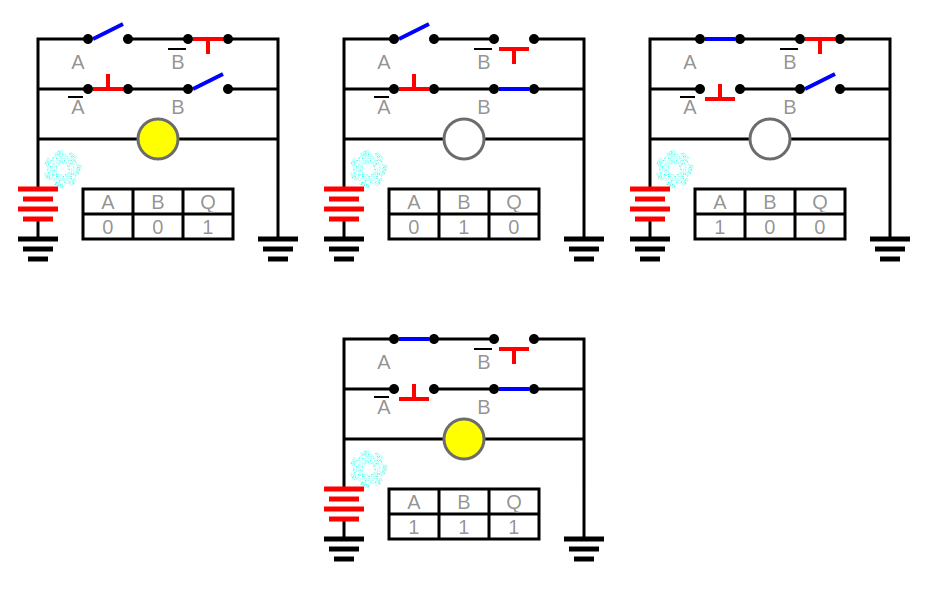
El circuito XNOR es la suma de los circuitos XOR y NOT. Por tanto, cogemos la tabla de la verdad del circuito XOR y negamos la salida, es decir, cambiamos los ceros por unos y los unos por ceros.
Su puerta lógica se representa así