Quien sea programador, entenderá el título de este post. ¿Son importantes los sistemas numéricos en la tecnología?
Esta pregunta es retórica. Sería como preguntar ¿el agua es húmeda? o ¿hace calor en el sol?
Evidentemente que son importantes para la tecnología. De hecho, si el Renacimiento no hubiera alumbrado a los matemáticos, estos no hubieran hecho los avances necesarios para que hoy tuviéramos Internet, la fibra óptica, el móvil y las redes sociales, de hecho no tendríamos ni las puertas automáticas o las vitrocerámicas.
Toda la tecnología se basa en las matemáticas. Las matemáticas aportan los sistemas numéricos a la tecnología para que los procesadores de los aparatos puedan ser programados. Todo, absolutamente todo que lleve un chip, es programable y sin los sistemas numéricos no podría hacerse.
Todo lo que un ordenador realiza, es posible gracias a que trabaja realizando sumas en sistema binario de forma incansable y certera. Por ello es importante comprender como trabajar con 3 sistemas números básicos en programación y tecnología:
- decimal
- binario
- hexadecimal
Muestro la tabla de equivalencias hasta el número 15 decimal de estos 3 sistemas numéricos. En negrita están los dígitos que usa cada sistema para hacer las operaciones y contar. A saber, 10 en decimal, 2 en binario y 16 en hexadecimal.
| DECIMAL | BINARIO | HEXADECIMAL |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
COMO PASAR DE UN SISTEMA A OTRO
DECIMAL a BINARIO
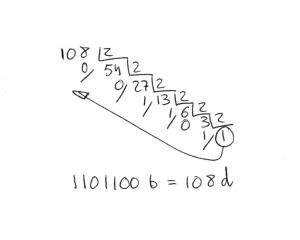 Se van haciendo sucesivas divisiones entre 2 -que es el número de dígitos que usa el sistema binario- sin sacar decimales, y nos detenemos cuando el cociente sea menor que 2, es decir, 1.
Se van haciendo sucesivas divisiones entre 2 -que es el número de dígitos que usa el sistema binario- sin sacar decimales, y nos detenemos cuando el cociente sea menor que 2, es decir, 1.
Luego escribimos el último cociente (siempre será 1) y los restos en orden ascendente.
DECIMAL a HEXADECIMAL
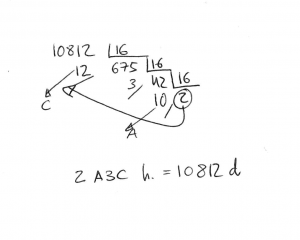 Se van haciendo sucesivas divisiones entre 16 -que es el número de dígitos que usa el sistema hexadecimal- sin sacar decimales, y nos detenemos cuando el cociente sea menor que 16.
Se van haciendo sucesivas divisiones entre 16 -que es el número de dígitos que usa el sistema hexadecimal- sin sacar decimales, y nos detenemos cuando el cociente sea menor que 16.
Luego escribimos el último cociente y los restos en orden ascendente, teniendo en cuenta que debemos traducir los restos a su homónimos en hexadecimal, es decir, si el resto es 10 pondremos A, etc.
BINARIO a DECIMAL
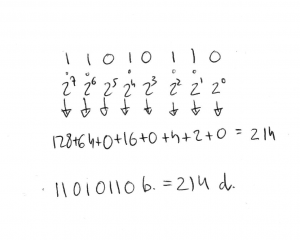 Escribimos el número binario separando sus dígitos. Debajo de los dígitos binarios colocamos las potencias de 2 desde el exponente 0 en adelante, de derecha a izquierda como podéis ver en la fotografía.
Escribimos el número binario separando sus dígitos. Debajo de los dígitos binarios colocamos las potencias de 2 desde el exponente 0 en adelante, de derecha a izquierda como podéis ver en la fotografía.
Luego multiplicamos las potencias de 2 por el dígito binario y sumamos los resultados.
BINARIO a HEXADECIMAL
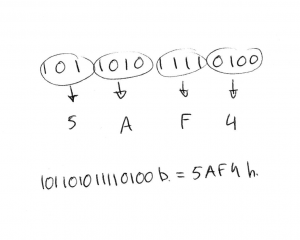 Agrupamos los dígitos binarios de 4 en 4 comenzando por la derecha. Luego buscamos su homólogo en hexadecimal en la tabla de equivalencias.
Agrupamos los dígitos binarios de 4 en 4 comenzando por la derecha. Luego buscamos su homólogo en hexadecimal en la tabla de equivalencias.
El primer grupo, el de la izquierda puede tener 1, 2, 3 o 4 cifras.
HEXADECIMAL a DECIMAL
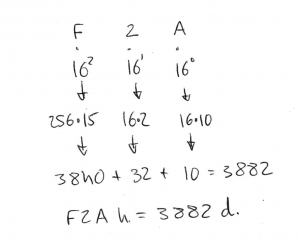 Escribimos el número hexadecimal separando sus dígitos. Debajo de cada uno colocamos las potencias de 16 desde el exponente 0 en adelante, de derecha a izquierda como podéis ver en la fotografía.
Escribimos el número hexadecimal separando sus dígitos. Debajo de cada uno colocamos las potencias de 16 desde el exponente 0 en adelante, de derecha a izquierda como podéis ver en la fotografía.
Luego multiplicamos las potencias de 16 por el homólogo en decimal del dígito hexadecimal y sumamos los resultados.
HEXADECIMAL a BINARIO
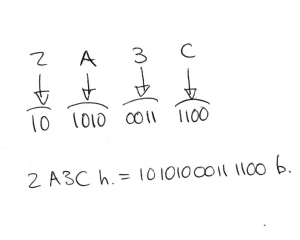 Para cada dígito hexadecimal debemos escribir su homólogo en binario pero con 4 cifras binarias, es decir que si debemos traducir el 4, que es el 100, pondremos 0100. Por tanto rellenaremos con ceros a la izquierda los que falten hasta 4 dígitos. Esto no será necesario en la primera cifra hexadecimal, la de la izquierda.
Para cada dígito hexadecimal debemos escribir su homólogo en binario pero con 4 cifras binarias, es decir que si debemos traducir el 4, que es el 100, pondremos 0100. Por tanto rellenaremos con ceros a la izquierda los que falten hasta 4 dígitos. Esto no será necesario en la primera cifra hexadecimal, la de la izquierda.

