Se llama ‘fracción generatriz‘ a la fracción que representa a cualquier número racional.
Toca sumergirse en el baúl de los recuerdos de nuestros estudios primarios y encontrar el conocimiento que nos transmitieron nuestros profesores los antiguos sobre los números. Recordemos aquella división de los números en racionales e irracionales.
- Nº racional –> aquel que puede expresarse por medio de una fracción
- Nº irracional –> aquel que no puede
A poco que pensemos, está claro que todos los números enteros son racionales porque pueden representarse en forma de fracción fácilmente si ponemos 1 como denominador, es decir,
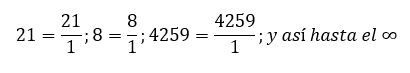
Veamos ahora los números decimales. Los números decimales pueden tener un número determinado de decimales o un número infinito de decimales.
CASO 1 –> número determinado de decimales
Este tipo de números sí que tienen fracción generatriz, que se forma de la siguiente forma:
- 2 decimales 2’34= 234/100
- 3 decimales 0’241=241/1000
- 4 decimales 3’9023=39023/10000
- n decimales =el número sin comas dividido entre un 1 seguido de n ceros
ejemplo:
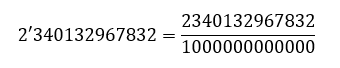
el número tiene 12 cifras decimales, luego se divide por un 1 seguido de 12 ceros
CASO 2 –> número infinito de decimales
Dentro del caso 2, podemos a su vez subdividirlo en otros dos casos:
CASO A –> no se repite ningún patrón en las cifras (nº irracionales)
Estamos ante el caso de los números irracionales ya que son los únicos que no pueden representarse en forma de fracción. Veamos los ejemplos más típicos de nº irracionales
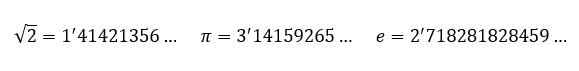
CASO B –> si 1 o varias cifras se repiten indefinidamente
Este caso es el de los números decimales periódicos. Tipos de números periódicos:
Periódicos puros
Aquellos en los que se repiten los decimales desde la primera cifra:
0’333…, 0’919191…, 0′ 460460460…, …
Por convención, en matemáticas ponemos un gorrito encima de las cifras que se repiten indefinidamente, quedando las del ejemplo como
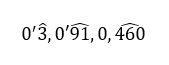
La fracción generatriz la calcularemos así:
-
-
- numerador –> el nº decimal sin la coma menos su parte entera
- denominador –> tantos 9 como cifras se repitan en el periodo
-
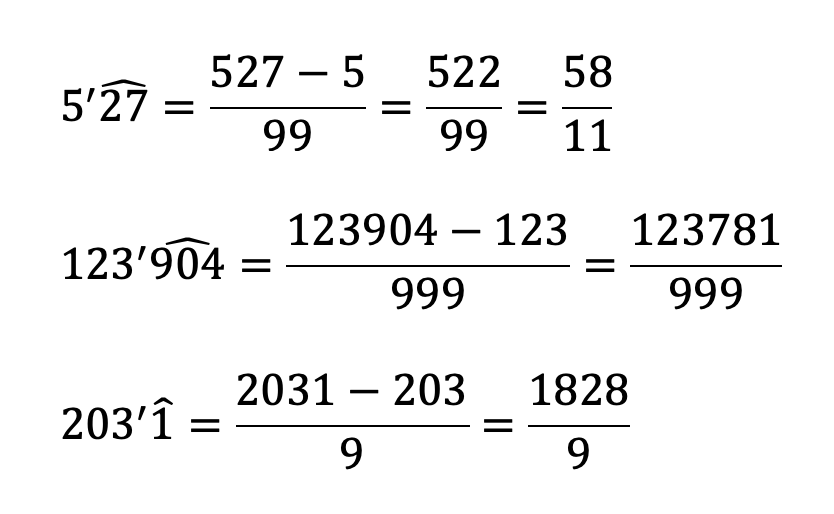
fracción generatriz de periódicos puros
Periódicos mixtos
Aquellos que tienen al principio una parte decimal que no se repite y luego una parte decimal que se repite indefinidamente:
0’2333…, 0’86242424…, 0’012595959…, …
Que usando el gorrito quedaría en:
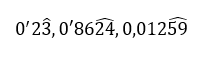
La fracción generatriz la calcularemos así:
-
-
-
-
- numerador –> el nº decimal sin la coma menos la parte que no se repite
- denominador –> tantos 9 como cifras se repiten en el periodo seguido de tantos 0 como decimales que no se repiten
-
-
-
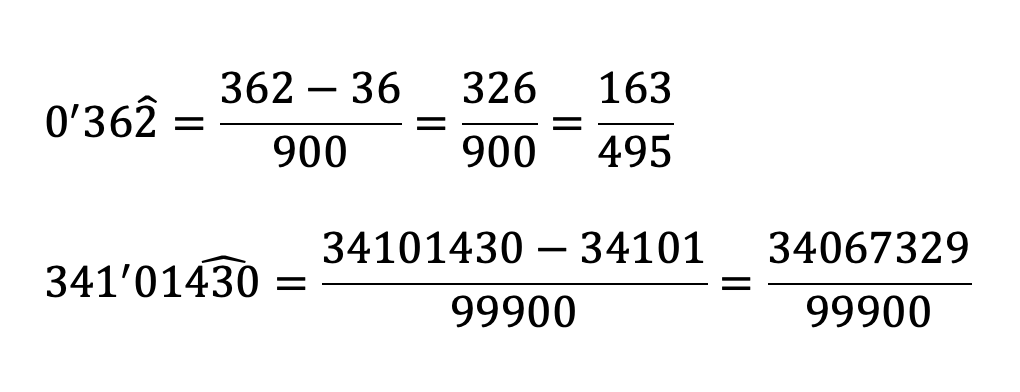
fracción generatriz de periódicos mixtos
[/et_pb_text][/et_pb_column]
[/et_pb_row]
[/et_pb_section]
